Esta é a segunda parte da matéria publicada em maio.
APRENDENDO E SE DIVERTINDO COM SINAIS
O processamento de sinais está por todos os lados. Celulares, TVs digitais, internet de alta velocidade, tocadores de música digital etc. nos cercam e não nos damos conta. Entretanto, esta é uma revolução silenciosa cuja presença em larga escala é fato relativamente recente. Há menos de 20 anos, um computador 486 foi o primeiro a transformar diretamente um arquivo digital em formato MP3 diretamente em música, e hoje por muito pouco, se compra um tocador de MP3 para mais de 24 horas de música ininterrupta.
Imagine então o que esta tecnologia recente pode fazer por um sistema de airbags que tem uma fração de milissegundo para saber a diferença entre um ruído do sensor e uma desaceleração real de colisão do veículo para disparo das bolsas infláveis. Mas, como isso funciona?
A matemática avançada envolvida na análise de sinais é bastante complexa, até mesmo para especialistas, de tal sorte que se torna inviável estudá-la na sua totalidade aqui. Mas isso não significa que não seja possível mostrar alguns fatos importantes e algumas técnicas avançadas aqui de uma forma acessível.
Um exemplo bem simples, mas interessante
Comecemos pensando num sistema bem simples e vamos dando um passo de cada vez. Peguemos o velocímetro digital de um carro. Hoje os sistemas de velocímetro por cabo de aço (tecnicamente uma árvore flexível) estão obsoletos e praticamente todos os carros usam sistemas de trens de pulsos para indicação de velocidade e distância percorrida. Se contarmos os pulsos, saberemos a distância percorrida dentro de uma escala. Se ficarmos contando os pulsos dentro de intervalos precisos de tempo, teremos a velocidade.
O trem de pulsos que sai do sensor tem a seguinte conformação:
Como nosso objetivo é obter a velocidade do carro, a onda pura e simples não nos interessa. Temos que estabelecer uma base de tempo dentro da qual contaremos os pulsos. Isso é o que faremos na próxima imagem. Os intervalos de tempo de contagem, que tecnicamente chamamos de tempo de amostragem, são delimitados pelas linhas tracejadas em azul.
Vamos começar pelo caso mais simples, mostrado pela onda A. Nela o tempo de amostragem coincide com o começo da onda, e ele também é um múltiplo da freqüência dela.
Vamos contar o trem de pulso no tempo de amostragem pelo ponto mais óbvio: pelo topo dos pulsos, indicados pelas setas vermelhas. Temos na imagem 3 períodos de amostragem e contamos 3 e 3, o que poderia significar 3 km/h.
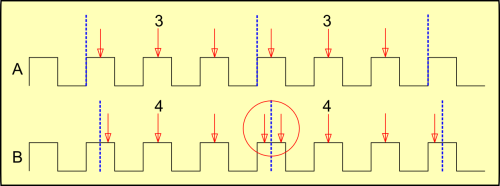
Entretanto, o trem de pulsos no caso mais genérico não tem obrigação de estar em sincronismo com os tempos de amostragem, e vemos isso na onda B. Vamos contar os pulsos.
Espere. Algo não vai bem. Agora estamos contando 4 e 4, mas a onda não mudou. Se a onda é a mesma, então deveríamos tirar a mesma medida, independente da nossa referência. Então, onde erramos?
Repare no círculo vermelho. Um pulso é dividido ao meio pelo limite de dois períodos de amostragem e ele é contado nos dois períodos, o que gera um erro de contagem. Precisamos encontrar outra forma de contar esses pulsos sem cair nessa armadilha.
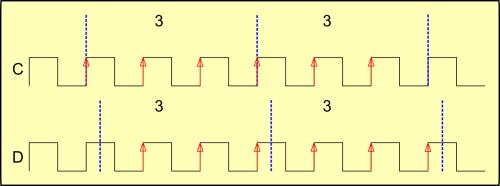
Uma forma é a que vemos na figura a seguir. Ao invés de contarmos os topos dos pulsos, contamos as mudanças de nível baixo para alto. Agora contamos 3 e 3, tanto com os períodos de amostragem em fase (onda C) como fora dela (onda D).
Esta técnica, chamada de “contagem de borda de subida” nos dá resultados precisos, e nela as larguras dos pulsos não é interessante para qualquer efeito de medida.
Na imagem seguinte, ondas E e F, temos a alternativa de contagem por borda de descida, igualmente eficiente.
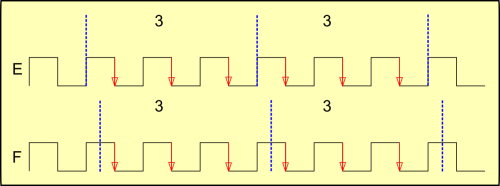
Tiramos daí algumas lições. Existem formas “certas” e “erradas” de avaliar sinais, e nem sempre a forma mais óbvia é a mais correta. Dentro do exemplo, estes fatos são bastante visíveis, mas existem grandes e valiosos projetos que fracassam porque partem de formas “erradas” de avaliar sinais fundamentais ao projeto.
E por que me referi a “certas” e “erradas” entre aspas? Porque uma forma “errada” pode ser útil em outras formas de análise, onde a “certa” pode não ser conveniente ou precisa. Tudo depende da aplicação.
Evitando falsificações
Considere a imagem escaneada desta nota antiga de 5 reais.
Esta nota, criada em 1994, lutava contra um determinado tipo de falsificação através de um equipamento bastante comum na época: as máquinas de fotocópia (“Xerox”).
Na imagem a seguir, vemos um detalhe da nota em alta resolução. A área clara não parece exibir nada de excepcional.
Entretanto, se passarmos a mesma imagem para preto e branco e com maior contraste, percebemos alguns padrões surgirem um pouco mais nítidos entre as linhas entrecruzadas da parte clara.
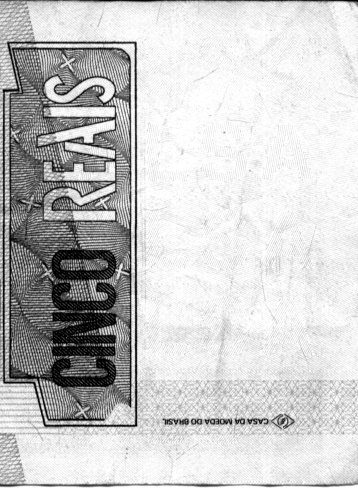
O leitor percebeu a sutileza do que foi impresso? Se não ficou claro, aqui vai uma ajuda:
(Dica: clique na imagem e use use a roda do mouse com a tecla CTRL do teclado para ampliar e perceber melhor os detalhes da imagem)
Pode parecer estranho, mas a antiga nota verdadeira de 5 reais possui algumas marcas da palavra “FALSA” impressas nela. No sistema de coloração utilizado na impressão da nota, este detalhe escapa ao olho humano, porém, quando mudamos o sistema de coloração para preto e branco, o maior contraste de cores torna o detalhe mais visível.
Repare que cada palavra “FALSA” possui um padrão distinto de linhas em contraste com o fundo. As linhas contidas no espaço das letras são perpendiculares às das linhas circundantes, e cada palavra possui um padrão diferente de inclinação de linhas. Há uma informação ali, e que se refere à inclinação das linhas, mas é sutil demais para ser percebida pelos olhos humanos.
A máquina de fotocópia tem um defeito em seu processo de cópia que privilegia a impressão das linhas horizontais, e estas são reforçadas quando a imagem da nota é copiada. Se as linhas das letras são horizontais e as circundantes são verticais, a máquina irá reforçar as linhas das letras e enfraquecer as circundantes, deixando a palavra “FALSA” escura em destaque contra um fundo claro. Se a nota for girada 90 graus, o efeito se inverte, e temos a palavra “FALSA” clara sobre um fundo escuro.
Para evitar que o falsário obtenha o padrão de linhas inclinando a nota, há várias marcas da palavra “FALSA” repetidas, mas cada uma com padrão de inclinação diferente, de sorte que qualquer inclinação que seja usada em relação à varredura da máquina sempre gerará uma palavra “FALSA” em contraste com o fundo, aumentando a segurança contra esse tipo de fraude.
Isto garante que sob diferentes condições de processamento da imagem da nota haverá mais chances de pelo menos uma das palavras ficar mais evidente.
A nota de 2 reais da mesma geração desta nota de 5, que foi lançada posteriormente, e mesmo a atual geração de notas já não possuem este mecanismo de segurança, pois os scanners de alta resolução não possuem esse defeito, e não funcionam como filtro.
Pode não parecer, mas esta é uma forma de processamento de sinais, e mostra o imenso repertório de técnicas que podem ser usadas para destacar um sinal de um ruído. No caso, usa-se um defeito conhecido das máquinas de fotocópia como filtro de sinal. Também é um bom exemplo de processo não digital de processamento de sinais.
Este é um bom exemplo de como diferentes tipos de filtro podem ser usados para separar sinais de ruídos, e mostra que não há técnicas certas ou erradas, mas sim as mais adequadas para cada caso.
Continuando a aprender
Voltando ao exemplo do velocímetro, os sinais que vimos até agora são muito particulares. O sinal de amostragem é um múltiplo preciso do trem de pulsos. Este é um caso bem particular.
O caso real é que o sinal não seja um múltiplo do sistema de amostragem. É quando ocorre um fenômeno bem curioso.
Vejamos na figura a seguir duas ondas, a G e a H. A G é uma ampliação contendo apenas os dois primeiros períodos de amostragem da onda H, onde são mostrados 8 períodos.
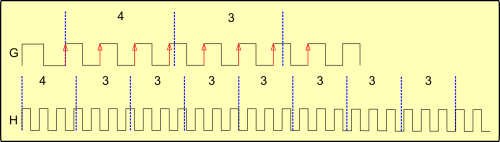
Na onda G, vemos que o primeiro período de amostragem conta 4 pulsos, contra 3 do período seguinte, usando o método por borda ascendente. Repare que apenas uma pequena parte de um pulso invade o primeiro período de amostragem, permitindo a contagem de 4. Este pulso já não é contado no período seguinte, mas a defasagem do pulso ao final do segundo período de amostragem está um pouco maior.
Na onda H vemos isso se propagar para os períodos seguintes. O que observamos é que se forma uma sequência de valores: 4,3,3,3,3,3,3,3,3. É uma leitura de 4 seguida de uma sequência de 7 leituras de 3. Se persistirmos nessa velocidade veremos essa seqüência se repetir continuamente.
Já percebeu que às vezes, andando em velocidade constante o velocímetro marca por exemplo 70 km/h, de repente mostra 71 e volta para 70? É exatamente este efeito. Mas este efeito não é apenas mera curiosidade.
Vamos pensar assim: podemos dizer que todas as leituras têm um valor base de 3 e mais 1 a cada 8 leituras. ou 3 + 1/8. Essa forma não é mera coincidência. Fazendo as contas de 3+1/8 temos 3,125.
Outra forma de vermos esses número é tirando uma média das leituras entre os 8 períodos de amostragem: (4+3+3+3+3+3+3+3)/8 = 25/8 = 3,125.
Ou seja, a velocidade real do carro é de 3,125 km/h.
Parece estranho. O mostrador tem resolução de 1 unidade, e ainda assim é capaz de apresentar um resultado muito mais preciso do que a da sua resolução.
Há uma lição muito importante e sutil a ser aprendida aqui. Normalmente mesmo engenheiros experientes acreditam que a informação do sinal está nas leituras diretas (4,3,3,3,3,3,3,3), porém isto não é real. Há informação não apenas nos valores instantâneos, mas também distribuídos ao longo da seqüência de leituras na forma como elas oscilam. A oscilação da leitura carrega informação e não é apenas ruído ou imprecisão do mecanismo de conversão e leitura.
A leitura instantânea do mostrador é imprecisa sobre a velocidade real inscrita no sinal, e o erro entre a leitura direta e a velocidade real se reflete nas oscilações de leitura, de forma que a informação como um todo seja expressa pelo sistema. Quando consideramos apenas as leituras instantâneas, estamos jogando fora uma boa quantidade de informação, impressa nas oscilações. O que parece ruído é parte da informação que jogamos fora.
Mais informação versus menos informação
Vamos pensar em um par de números, 1 e 9, por exemplo. A média entre os dois números é 5. Mas 5 também é a média do conjunto 2 e 8, ou do conjunto (2,4,6,8). A média aritmética de um conjunto de de números é uma forma de redução de informação, mantendo uma característica fundamental do conjunto completo. É fácil obter a média a partir do conjunto de dados, mas o caminho inverso, de obter os dados a partir da média é impossível, porque as possibilidades são infinitas.
Existe portanto uma lei no processamento de sinais que diz que é possível obter menos informação a partir de mais informação, mas não é possível obter mais informação a partir de menos informação.
Esta lei é óbvia, mas nem todas as técnicas que a envolve são exatamente óbvias. Tivemos uma rápida visão disso com o exemplo do velocímetro. A informação completa (a velocidade precisa com todas as casas decimais) não é a que é mostrada pelo mostrador, mas é representada pela seqüência de leituras.
Entretanto, nem sempre esta lei é perceptível pelas pessoas. Na época da popularização do MP3, dado que a maioria dos usuários ainda tinham conexões discadas e lentas, se popularizaram as músicas com bit rate de 128 kbps. Entretanto a qualidade da gravação a 128 kbps deixava muito a desejar. O tempo passou, as conexões com a internet aumentaram em muito sua velocidade, permitindo que arquivos maiores pudessem ser trocados com maior facilidade. Então disseminou-se a idéia que as músicas em MP3 de bit rate mais alta, em especial as de 256 e 320 kbps, eram bem superiores ao dos tradicionais arquivos de 128 kbps, e logo músicas com essas taxas se popularizaram nos mecanismos de compartilhamento. Em princípio, isso não está errado, mas levou a más interpretações.
Uma análise de muitos desses arquivos de elevada bit rate compartilhados revelou que eram meras versões dos arquivos de 128 kbps populares. É como se as pessoas acreditassem num passe de mágica que transformaria o arquivo com qualidade deficiente de 128 kbps em um arquivo de alta qualidade apenas convertendo-o para o padrão de 320 kbps. Isso não ocorre. Na melhor das hipóteses, o arquivo de 320 kbps assim gerado tem a mesma qualidade do de 128 kbps original.
A música de alta qualidade a 320 kbps é a obtida a partir da gravação original, seguindo o princípio que é possível obter menos informação a partir de mais informação, mas não a partir de um arquivo de 128 kbps, onde teríamos mais informação obtida a partir de menos informação.
É fácil acreditar que a perda de informação seja um fenômeno negativo, mas nem sempre é assim. O sistema de medição do combustível no tanque é um bom exemplo de como a redução da informação pode ser positiva. Enquanto o carro se movimenta, o combustível é agitado dentro do tanque, e a bóia do sensor é movimentada continuamente para cima e para baixo. Se o indicador no painel acompanhasse fielmente o movimento da bóia, o motorista nunca teria uma avaliação realista do conteúdo do tanque. Um leitor superamortecido mostra um valor médio de forma mais consistente e dá uma idéia melhor de autonomia para o motorista.
Há muitas implicações tecnológicas para esta lei. Voltando ao exemplo do velocímetro nas ondas G e H, vemos que o instrumento tem uma capacidade limitada de avaliar a informação completa da onda de pulsos, e que conseguimos reconstituir a informação total a partir de várias leituras parciais consecutivas do mostrador.
A informação total está impressa em cada pulso da onda, mas a forma de medirmos possui limitações, o que é o mesmo que obtermos menos informação a partir de mais informação, e não conseguimos projetar com precisão a velocidade real a partir de uma única leitura do mostrador. Conseguimos isto através de várias leituras consecutivas, porém com uma sutileza a mais. Cada leitura é feita a partir de uma amostragem feita com uma fase levemente diferente da anterior, de forma a abarcarmos a informação completa ao explorar a onda cada vez em uma posição diferente.
Assim, se temos um instrumento de baixa resolução e queremos obter uma informação com alta resolução, não conseguimos obter a partir de uma única leitura, porque não é possível obter mais informação a partir de menos informação. Porém, se obtivermos várias leituras de baixa resolução da mesma informação, porém com leve defasagem a cada leitura, obtemos mais informações parciais a partir das quais podemos recompor a informação completa.
Esta mesma técnica básica pode ser aplicada em uma enormidade de aplicações, de tal forma a obtermos informações muito mais precisas do que a limitada resolução dos instrumentos utilizados.
Uma aplicação desta técnica muito importante, surgida nos anos 1960 com a pesquisa espacial, era a obtenção de fotos de alta resolução a partir de satélites.
Por mais que tenhamos câmeras fotográficas atuais de dezenas de megapixels, uma foto não mostra grandes detalhes a centenas de metros. Da mesma forma, não é possível tirar uma foto com resolução de alguns metros da superfície da Terra a partir de uma única foto tirada de um satélite. Então, como são feitas as conhecidas fotos em alta resolução?
Na câmera do satélite cada pixel cobre uma área muito grande da superfície do planeta e cada foto sozinha não é muito útil. Porém, cada pixel representa uma média da luz da área fotografada. O pixel da câmera do satélite obtém uma única informação a partir de uma grande área da superfície. Ele obtém menos informação a partir de mais informação.
Quando o satélite se move, ele bate uma série de fotos, cada foto um pouco deslocada da anterior, e cada pixel experimentava uma leve mudança na luminosidade porque a área fotografada era um pouco diferente. A pequena parte nova fotografada havia sido fotografada na foto anterior pelos pixels vizinhos, assim como a parte descartada da foto anterior migrou para outros pixels próximos. Quanto menor a distância entre duas fotos consecutivas, quanto maior a resolução de cor e brilho do pixel e quanto mais fotos por série, mais informação é obtida para ser processada por um computador e obter uma foto de alta resolução.
O ato de tirar uma foto é uma forma de obter menos dados a partir de mais dados. Para reconstituirmos ao menos parte da informação necessária, tira-se várias fotos levemente defasadas umas das outras como caminho para se obter a informação suficiente para reconstituição da imagem original em alta resolução.
Técnicas semelhantes são usadas pelos sensores usados em carros autônomos para mapear em 3 dimensões o ambiente circundante, incluindo a definição objetos móveis dentro desse espaço.
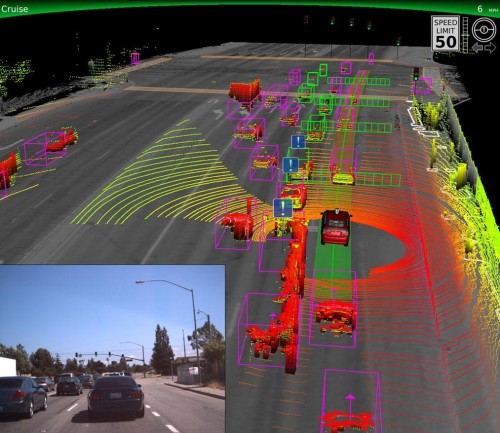
Do ponto de vista biológico, temos dois olhos para uma percepção do espaço em 3 dimensões, sendo a distância entre nossos olhos importante nesse processo. Porém, quanto mais afastados forem os objetos, menor nossa capacidade de percebê-lo em 3 dimensões.
O mesmo pode ser dito dos nossos ouvidos. A distância entre eles permite ao cérebro comparar a mesma onda sonora com uma pequena defasagem entre os sinais dos dois ouvidos e com isso perceber a direção de onde vem. É um processo tão sofisticado que nos permite reconstruir um espaço sonoro onde podemos dizer onde está cada elemento sonoro à nossa volta. Entretanto, assim como na visão, a reconstrução do espaço sonoro tem limitações. Sons graves não são percebidos com direcionamento e é por isso que aparelhos de som modernos têm apenas uma caixa de subwoofer.
Digitalização
Embora as técnicas de processamento de sinais analógicos já tenham algumas décadas, são as técnicas digitais que hoje predominam, graças ao poder de cálculo e à flexibilidade do computador.
Porém, o computador não consegue manipular diretamente um sinal, mas sim uma imagem numérica dele. Isso é feito através da digitalização do sinal. A digitalização é feita colocando o sinal sobre uma escala de amplitude e o sinal é comparado com esta escala em passos iguais de amostragem (onda I).
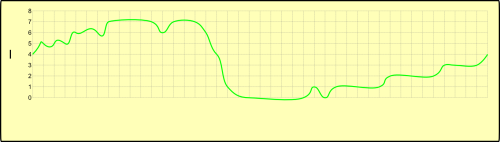
O resultado é uma seqüência numérica na memória do computador. A seqüência numérica obtida pode ser armazenada e manipulada livremente pelo computador, e é facilmente reconstituída (onda J).
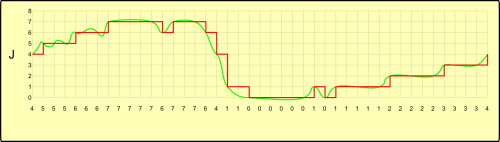
Aqui é importante notar algumas coisas. A onda I, analógica, é contínua no tempo e na amplitude, porém a onda digitalizada possui não uma, mas duas discretizações, uma na amplitude e outra no tempo. Aqui é o caso de se obter menos informação a partir de mais informação, e uma vez digitalizada, a onda reconstituída (a J, vermelha) nunca será idêntica à analógica (a J, verde).
Em tese, o sistema de digitalização do sinal só recuperaria o sinal integralmente com uma resolução de amplitude infinita e tempo de amostragem igual a zero.
Este é o argumento que os puristas usam para afirmar que o som do CD sempre será inferior ao som do LP analógico. Entretanto há um fenômeno que anula este efeito de perda de informação.
Todo sistema tem uma velocidade-limite de resposta, e essa velocidade limita a forma como ele reage ao sinal. Qualquer variação do sinal mais rápida que esse limite de velocidade do sistema é simplesmente ignorada por ele.
Pense no caso de olhar um pássaro voando no céu. Este é um processo analógico contínuo no tempo e no espaço. Mas num filme não temos uma gravação contínua. Temos a exibição de 25 fotografias por segundo, o que é suficiente para percebermos como uma visão contínua de movimento.
Esta propriedade de um processo discreto ser percebido como contínuo por um sistema se a freqüência de amostragem for maior que a de resposta do sistema, se aplica a qualquer sistema dinâmico. É ela que torna a digitalização de sinais possível e útil.
Voltando ao caso do CD, o som da música é digitalizada em um formato de dois canais, com taxa de amostragem de 44.100 Hz e resolução de amplitude de 65.536 níveis. Isso é suficiente para que a grande maioria das pessoas não diferencie um som natural do sinal digitalizado reproduzido em equipamentos de qualidade.
E a reprodução do CD é bem simples. Basta ler a seqüência de amostragem e um chip transforma diretamente a seqüência numérica gravada no disco num sinal analógico para ser reproduzido pelo amplificador. Por isso o CD se tornou um reprodutor de música tão popular.
Entretanto, até hoje a questão da recuperação do sinal original a partir do sinal digitalizado ainda é uma questão pouco reconhecida. É o que vemos nas ondas K. A partir da onda digitalizada (em vermelho) “quadrada”, é possível interpolar um sinal mais suave, “arredondado” (em azul). Este sinal é especulativo, já que a digitalização perdeu informações sobre o sinal original (em verde), e não é possível recuperá-lo com perfeição, porém é um sinal com menor erro do que o sinal digitalizado puro.
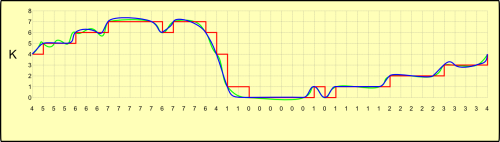
Em muitos sistemas, isso não é importante, como o caso da alimentação de motores elétricos automobilísticos, onde a onda digitalizada pode ser utilizada diretamente. Mas no caso de sinais de áudio, isso é importante para a manutenção da qualidade sonora. Entretanto, obter o sinal digitalizado direto é fácil, mas “arredondá-lo” apropriadamente é mais complexo e caro, e muitos equipamentos de áudio usam o sinal digitalizado direto por questões de custo.
Este foi o caso do iPod versus o iPhone. O iPod foi criado para ser um tocador de música digital de alta qualidade, especialmente nos modelos mais caros. Para isso, ele contava com um chip conversor analógico/digital (DAC, Digital Analogic Converter) de alta qualidade que “arredondava” os sinais de saída.
Quando a Apple criou o iPhone, o novo aparelho tinha uma série de requisitos diferentes do iPod por ser um aparelho multiuso. Havia compromissos com custo, espaço interno e consumo de bateria, três coisas que juntas obrigaram a Apple deixar o DAC do iPod de fora do projeto. Entretanto, pouca gente notou a diferença, e o iPhone “matou” o iPod sem receber o DAC de alta qualidade mesmo nos modelos de topo mais recentes. Portanto, diferentemente do que muitos dizem, o iPhone nunca foi um substituto direto do iPod.
Outra forma de “arredondar” sinais é a técnica de anti-aliasing aplicada às imagens digitais. Assim como no sinal de som, a imagem original se apresenta por demais “quadrada”, e fica nítida a percepção dos pixels da tela. A impressão que passa é que a imagem está cheia de “degraus”.
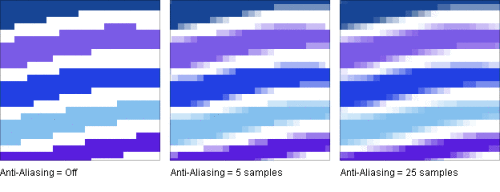Com o anti-aliasing, cada pixel é reprocessado em função dos pixels vizinhos e fica com uma cor intermediária entre a original e a média da vizinhança. O resultado é uma imagem mais compreensível, menos “dura”, “redonda”, sem tanta aparência de “degraus”, porém é uma imagem mais difusa.
Espremendo sinais
Observe a onda digitalizada L. Observe a seqüência numérica do sinal digitalizado. Vemos nela uma série de números repetidos entre amostragens consecutivas.
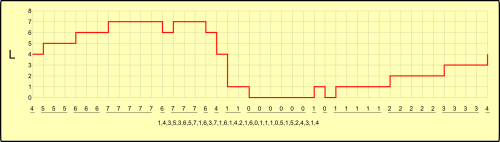
Uma vez obtida a seqüência de digitalização, vamos usar o computador para manipular esta seqüência. A partir desta seqüência de números simples de amplitudes em seqüência, vamos criar uma seqüência de pares de números, onde o primeiro representa o número de repetições de amostragens consecutivas e o segundo representa a amplitude a ser repetida. Vemos a nova seqüência abaixo da seqüência original.
No sinal digitalizado vemos que o primeiro par é (1,4). É uma perda, pois usamos dois números para representar apenas um. Entretanto, o par seguinte (3,5) usa dois números para representar três, o que empata o espaço gasto com o primeiro par. Acompanhando ao longo de toda digitalização, vemos que este formato de representar o sinal economiza espaço em relação à onda digitalizada original. Este processo é o que chamamos de compressão.
É importante notar que a seqüência comprimida permite recuperar o sinal amostrado com perfeição. É o que chamamos de compressão sem perdas, onde usa-se menos dados para representar a mesma informação. Os sistemas de compressão sem perdas são mais uma prova a mais de que a informação de um sistema está distribuída sobre toda seqüência numérica e não localizada número a número.
Quem pensar em programas de compactação de arquivos tipo ZIP e RAR não estará enganado. Arquivos são seqüências de números dentro dos computadores assim como sinais digitalizados, e é possível usar as mesmas técnicas de compactação de sinais aos arquivos.
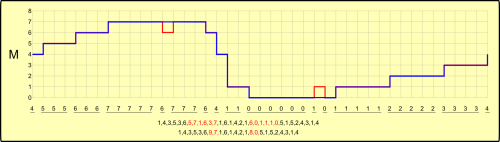
Na onda M vemos que a onda em azul se sobrepõe à vermelha, com a exceção de dois pequenos picos. Estes picos separam duas longas seqüências de amostragens de mesma amplitude, e quando manipulamos a seqüência, “aplainamos” a amostragem, de tal sorte que toda seqüência pode ser representada por apenas um par de de números. O resultado desta manipulação aparece na comparação entre as duas seqüências de sinal compactado. Na primeira, sem perdas, vemos dois trechos marcados em vermelho que são substituídos por dois pares, também em vermelho, na nova seqüência compactada, desta vez com perdas.
Se por um lado temos uma perda de informação para reconstrução do sinal a partir da segunda seqüência, obtivemos por outro lado uma maior compressão do sinal dentro do computador. Este método é chamado de compressão com perdas.
Podemos pensar que os métodos de compressão com perdas são ruins, mas tudo depende da aplicação. Um exemplo disso está na telefonia celular. O ouvido humano escuta na faixa de 20 Hz a 20.000 Hz, mas apenas uma pequena faixa dessas freqüências são necessárias para a compreensão da fala. Eliminado as freqüências desnecessárias e simplificando os sinais dentro da faixa da fala, é possível conseguir alta compressão do áudio sem que o sinal tenha perda significativa de compreensão por quem ouve. Num sistema de telefonia celular, onde o mesmo canal de rádio tem que sustentar o maior número de conversações simultâneas, isso é mais importante que um áudio perfeito.
Como o próprio nome diz, o sinal comprimido possui uma perda de informação sobre o sinal original, o que causa uma perda de qualidade do sinal recuperado. Esta perda de qualidade é característica do tipo de sistema de compressão/descompressão utilizado. Ainda assim é possível obter um sinal comprimido com perdas de melhor qualidade.
Quando comprimimos o sinal digitalizado uma primeira vez, podemos obter de volta um sinal recuperado da descompressão que terá distorções sobre o sinal original. Se subtrairmos do sinal recuperado o sinal original obtemos um sinal de erro, chamado de “ruído de compressão”. Se somarmos este sinal de ruído ao sinal original e refizermos a compactação, obteremos um novo sinal compactado com perdas e um novo sinal recuperado. Durante o processo de compactação e descompactação, o ruído de compressão age no sentido de reduzir o novo ruído de compressão. Este processo pode ser repetido para reduzir ainda mais o ruído de compressão, mas há um limite para a aplicação desta técnica, quando o ruído de compressão se estabiliza num certo patamar.
Aqui temos uma aplicação comercial sutil. Dois modelos de câmera fotográfica do mesmo fabricante podem usar o mesmo conjunto ótico e a mesma eletrônica para aumentar o fator de escala de produção e baixar custos, porém a diferença entre o modelo mais caro e o mais barato está na rotina que retrabalha a imagem compactada de forma a obter uma imagem recuperada de melhor qualidade no modelo mais caro que é ausente no modelo mais barato.
É evidente que o custo de aplicação desta rotina no modelo mais barato é praticamente nulo, mas é praticado como forma de diferenciação do produto no mercado. Esta técnica de diferenciação é conhecida como “anti-feature”, e é hoje classificada como uma parente próxima das obsolescências programada e percebida.
Uma deficiência dos sistemas de compressão com perda surge no processamento e manipulação do sinal. Cada vez que o sinal é descompactado para depois ser novamente comprimido, há uma perda de qualidade do sinal. Se o sinal sofre vários ciclos de tratamento, compressão e descompressão, ele estará deteriorado ao final do processo.
A recomendação que se faz é que quando se for manipular vídeos, imagens e sons, que sejam manipulados na maior resolução possível, e depois reduzidos para o formato desejado.
Há um fato estranho sobre o sinal compactado de alta qualidade. Quanto mais alta a qualidade do sinal com perdas recuperado, mais o sinal compactado estará matizado pelo ruído de compressão, e menor a sua fidelidade ao sinal original neste formato. Assim, quando queremos mesclar dois sinais compactados com perdas, como mesclar fotos ou sobrepor uma música como tema para um vídeo com som original, o mais fácil é recuperar os sinais compactados, adicioná-los e recompactar o sinal obtido mas com degradação da qualidade do sinal, ou então apelar para algoritmos complexos que permitem a adição diretamente no formato compactado para reduzir as perdas de um novo processo de compactação.
Esta é uma diferença entre programas de edição de vídeos, imagens e sons para uso profissional e amador. Os editores amadores são mais leves, rápidos e fáceis de programar que os profissionais, e por isso são mais baratos, mas isso tem um custo maior na qualidade do sinal compactado obtido.
Aqui termina esta aula elementar sobre processamento de sinais, fundamental para a compreensão dos carros do futuro, onde cada vez menos haverá dispositivos mecânicos e os sincronismos e automações serão mantidos por uma inteligência digital que percebe o mundo e atua sobre ele recebendo e enviando sinais.
AAD
