“Era uma vez, João e Maria, filhos pequenos de um lenhador que viviam numa casinha à margem da floresta. O pai sempre alertou dos perigos da floresta às crianças, mas se aventurar nela era a grande brincadeira dos dois. João era destemido, mas Maria era mais prevenida, e cada vez que iam brincar na floresta, Maria ia até o riacho e enchia os bolsos com pedrinhas brancas. Conforme andavam pela floresta, Maria deixava uma pedrinha aos pés de uma árvore, e assim marcava o caminho de volta para casa.
Um dia, João estava tão ansioso para brincar na floresta que nem deixou Maria pegar as pedrinhas. A única coisa que Maria tinha nos bolsos era um pão, e ela usou migalhas para marcar o caminho. Mas quando terminaram de brincar, Maria percebeu que os passarinhos tinham comido as migalhas de pão. Os dois estavam perdidos na floresta…”

A história de João e Maria (“Hänsel und Gretel” no original) é antiga, parte das histórias de fadas de tradição oral coletadas pelos irmãos Grimm, e por isso tem muitas versões como esta.
Histórias infantis como estas não existiam apenas para divertir, mas também para passar importantes lições para as crianças. Porém ela carrega uma sutil lição para a engenharia de trânsito moderna.
Há muito que os leitores do AE que me acompanham me veem criticando constantemente a obsoleta engenharia de tráfego por não atender mais as necessidades atuais do sistema viário urbano. Mas será que há algo mais além dos livros canônicos da área?
Certamente há, mas será preciso “chutar o pau da barraca” e “pensar muito fora da caixa” para perceber algumas relações interessantes e sutis do fluxo de trânsito , e mais que isso, achar novas aplicações e soluções ligadas a elas.
O que vou descrever aqui não está em livros canônicos da engenharia de tráfego. Este é um grande projeto de mobilidade urbana, fruto de estudos pessoais de diversas áreas que convergem de forma inusitada para o estudo da microestrutura do fluxo de tráfego, e criam uma nova maneira dele ser pensado. Porém estes estudos pessoais estão em sintonia com áreas de investigação científica bastante recentes.
Hoje sai de cena o autor-crítico e entra o autor-pesquisador.
O problema da velha engenharia de tráfego
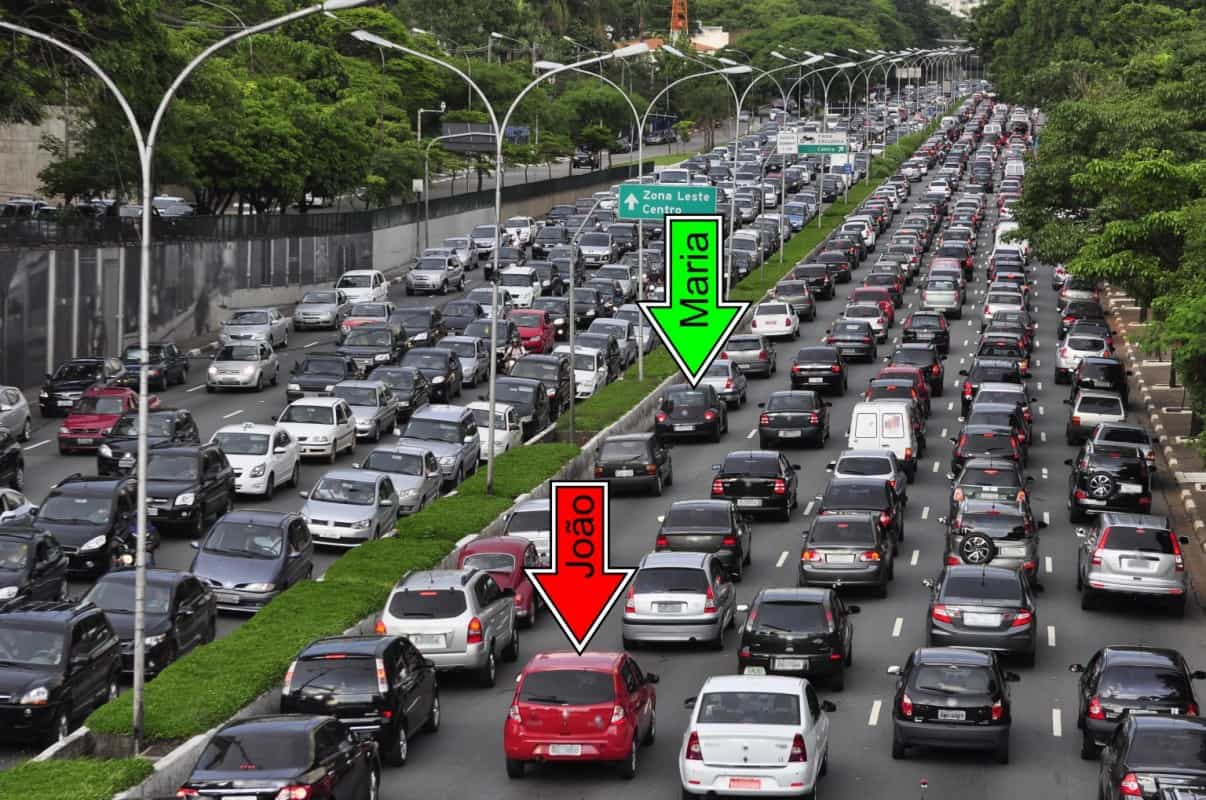
Olhe para a foto a seguir. Ela mostra a longa fila de carros numa avenida num fluxo bem pesado de de tráfego.

O que podemos dizer sobre esse fluxo em especial? Há muito pouco além de dizermos que é um agrupamento aleatório de carros. Do pouco que podemos dizer é que se alinham conforme as faixas de rolamento demarcadas na avenida, e que seguem um após o outro já que não podem ocupar o mesmo espaço ao mesmo tempo.
De resto, a observação dia após dia deste fluxo não aparenta revelar mais nada que pudesse ser utilizado. A sequência de veículos nunca se repete, e a lógica e a observação indicam que a distribuição destes veículos é completamente aleatória. Para estes casos, a única ferramenta disponível para análise é a estatística.
Estão aí criadas as bases para a engenharia de tráfego, cujos primeiros estudos acadêmicos datam de quase um século atrás. O resultado são médias, mínimos, máximos e gráficos como o que vemos, onde o fluxo é tratado como uma massa homogênea, onde cada carro é igual aos demais e sem que se consiga estabelecer qualquer tipo de relação entre eles.
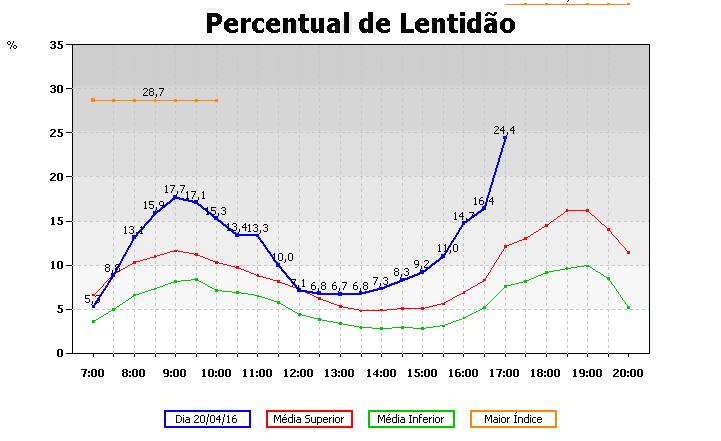
Este é o motivo para os limites que andam tornando esta abordagem rapidamente obsoleta. Há comportamentos importantes que o estudo estatístico não explica, como a onda de parada fantasma.
Este fenômeno, um comportamento não linear do fluxo que se propaga no sentido contrário ao do fluxo que faz com que os carros alternadamente andem e parem ao invés de sustentarem um fluxo constante de baixa velocidade.
A onda de parada fantasma não pode ser explicada pela estatística porque é um fenômeno relacionado com a microestrutura do fluxo, do relacionamento de veículo a veículo e da dinâmica de cada um deles individualmente.
Mas será que o fluxo de trânsito teria outras propriedades importantes relacionadas com sua microestrutura, ou o fluxo é, como defendem as antigas teses da engenharia de tráfego, uma massa caótica e estatisticamente homogênea de veículos, impossível de ser caracterizada internamente? Pois novas teorias científicas recentes e tecnologias vem jogando uma nova luz a esta questão.
A matemática dos 6 graus
O autor húngaro Frigyes Karinthy defendeu em 1929 um conceito muito estranho na época. Ele defendeu que, apesar do grande número de pessoas, o relacionamento de conhecimento entre elas faria com que uma pessoa estaria ligada a qualquer outra no mundo, por mais desconhecida que fosse, por apenas 6 pessoas conhecidas intermediárias. Assim, uma pessoa poderia enviar uma mensagem para esta outra passando para um conhecido, que passa para outro conhecido, …, até que chegue ao destinatário.
Baseado em trabalhos intermediários feitos sobre a proposta de Karinthy, em 1998 o Dr. Duncan J. Watts e seu orientado de doutorado Steven Strogatz publicaram um artigo que revolucionaria o estudo das redes, o que ficou conhecido como “Teoria do Mundo Pequeno”.
A Teoria do Mundo Pequeno mostrou que os nós de rede aleatória podem estar a poucos saltos entre nós intermediários até atingir qualquer outro nó da rede. O número de nós da rede poderia ser gigantesco, mas a “distância” entre quaisquer nós poderia ser pequena através das interligações entre eles.
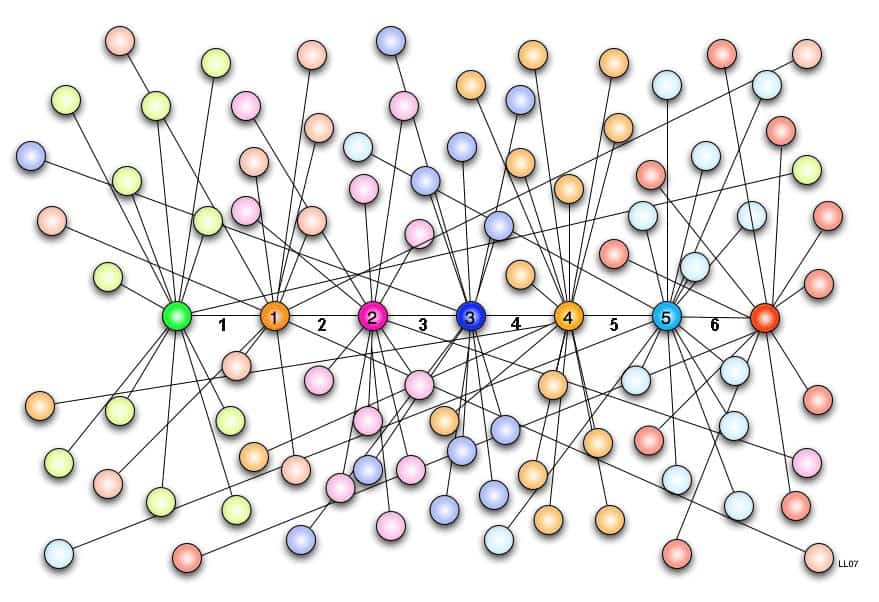
Redes de mundo pequeno foram encontradas por todos os lados. Não apenas relações sociais entre indivíduos geram mundos pequenos, mas a relação entre genes dentro do código genético, de neurônios no cérebro, entre um bilhão de transístores dentro de um processador.
O mundo pequeno do fluxo
Poderia o fluxo de trânsito apresentar uma estrutura de mundo pequeno? Como, se os carros que visualizamos à nossa volta são sempre diferentes e de pessoas desconhecidas?
Vamos começar pensando em um personagem fictício, mas bastante comum, o João. Como muita gente, João trabalha em horário comercial, e precisa se deslocar de sua casa até seu ambiente de trabalho. E ele toma sempre o mesmo caminho para chegar até lá.
Enquanto se desloca, João passa por muitas pessoas que seguem pelas mesmas vias.
Agora vamos imaginar um segundo personagem: a Maria. Ela mora a alguns quarteirões de João, trabalha no prédio ao lado e segue pelo mesmo caminho quase na mesma hora. Mas João e Maria não se conhecem, apesar de todas as coincidências.
Apesar de terem de chegar no mesmo lugar praticamente ao mesmo tempo, dia após dia, há todo um conjunto de fatos aleatórios que mantém João e Maria afastados no fluxo de tráfego. Um dia Maria está 100 metros à frente de João, outro dia, 200 metros atrás, e num outro dia ela pode estar ao lado dele. Porém, no meio de tantos outros carros, João pode simplesmente nunca notar a presença constante de Maria e vice-versa.
Da mesma forma, é humanamente impossível ao técnico que estuda o trânsito individualizar cada carro e estabelecer relações com ele. Daí a limitação das teorias canônicas da engenharia de tráfego.
Quando pensamos na questão do fluxo de uma maneira mais abrangente, o termo “horário de pico” se refere a um maior fluxo de tráfego causado pelas pessoas que vão e voltam do trabalho mais ou menos no mesmo horário e passam pelo mesmo caminho, gerando uma saturação da via.
Uma parte significativa de veículos do fluxo de tráfego, tratada pela velha engenharia de tráfego como algo homogêneo e disforme, na verdade é uma grande rede social do tipo mundo pequeno, onde estranhamente as pessoas se relacionam intimamente todos os dias, mesmo sem se conhecerem. Esta é a primeira conclusão importante sobre a microestrutura do fluxo de trânsito.
O conto de João e Maria e as formigas
A história de João e Maria, contada há séculos, tem muitas similaridades com o que vem sendo aprendido com as formigas. Elas usam técnicas muito simples que geram interação social complexa e manifesta uma grande inteligência coletiva de forma parecida com a história de João e Maria.
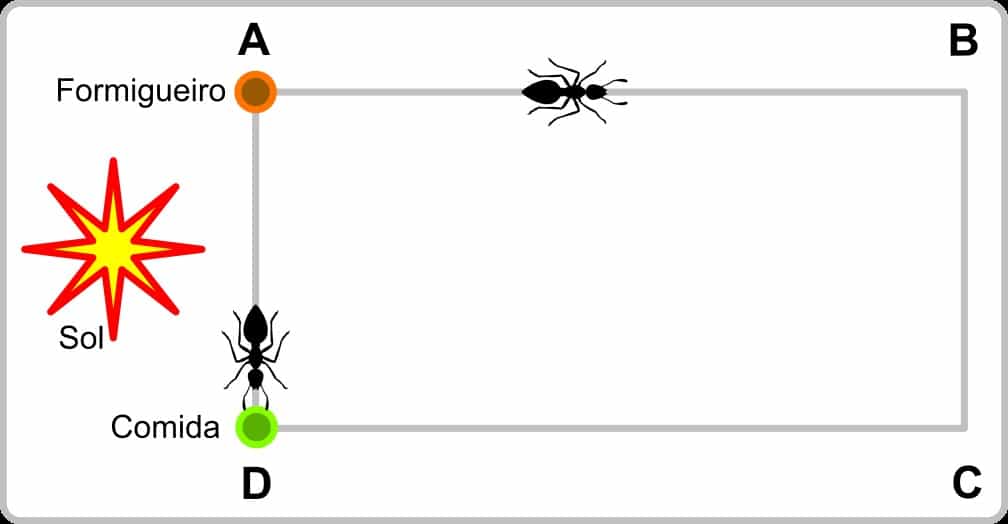
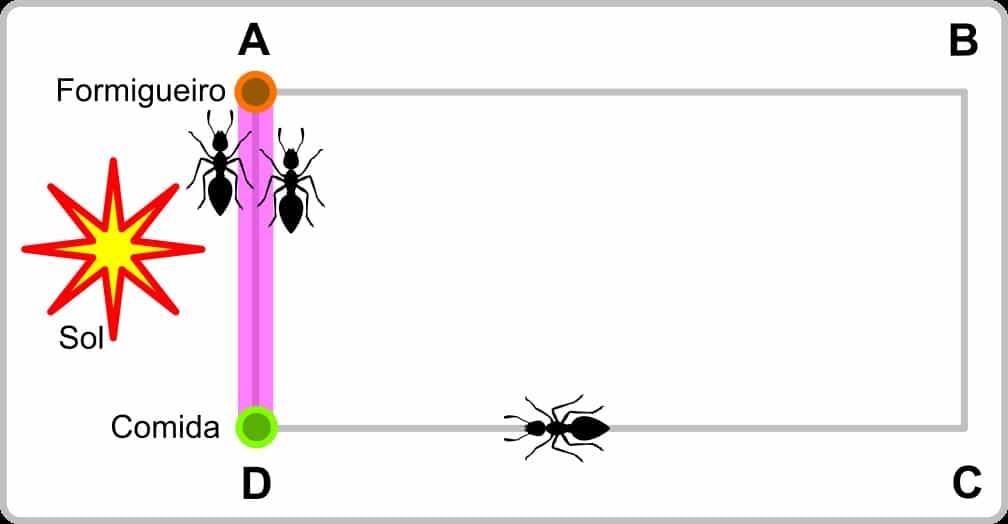
Vamos olhar o esquema a seguir. Neste esquema, o formigueiro está no ponto A, enquanto o alimento está no ponto D. Ligando estes dois pontos, temos dois caminhos, o mais curto A-D e o mais longo A-B-C-D.
Num determinado instante, duas formigas partem para encontrar alimento, uma seguindo o caminho A-D e outra o caminho A-B-C-D. Enquanto caminham com a mesma velocidade, as formigas usam o sol como referência para saber onde se encontra o formigueiro.
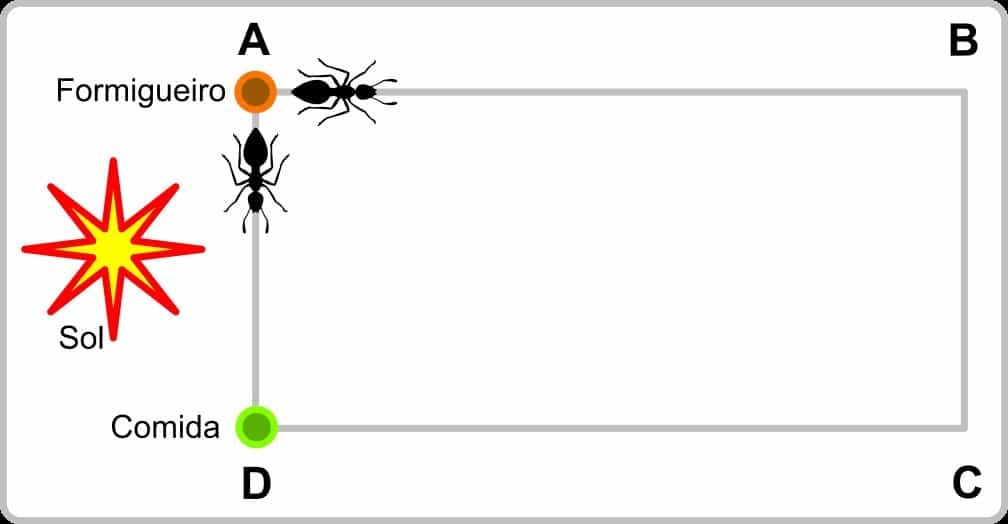
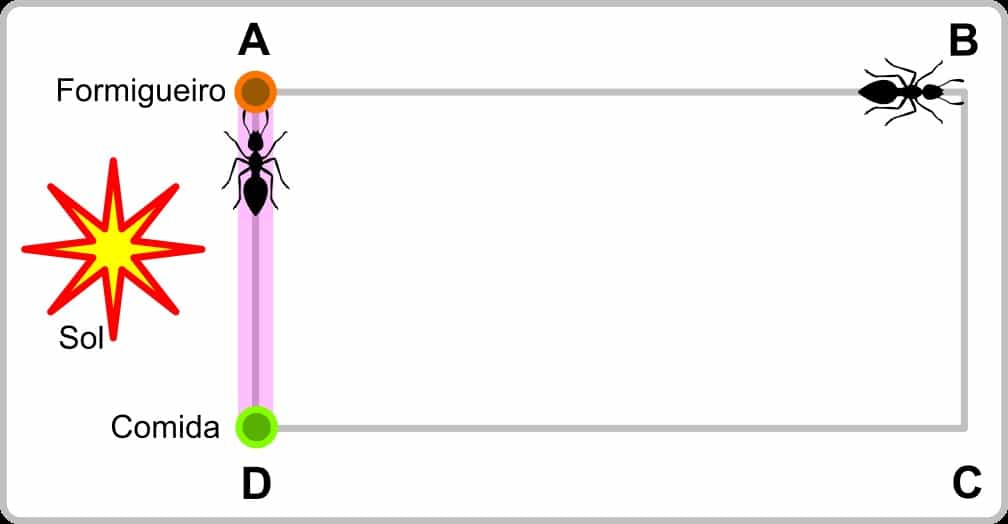
Em determinado instante, a formiga que segue pelo caminho A-D chega em D e encontra alimento. Ela então pega uma porção deste alimento e retorna para o formigueiro.
Porém, como na história de João e Maria, a formiga vai marcando o caminho conforme retorna. A formiga possui na extremidade das patas traseiras glândulas que liberam um tipo feromônio, uma espécie de perfume, que é deixado no solo a cada passo da formiga.
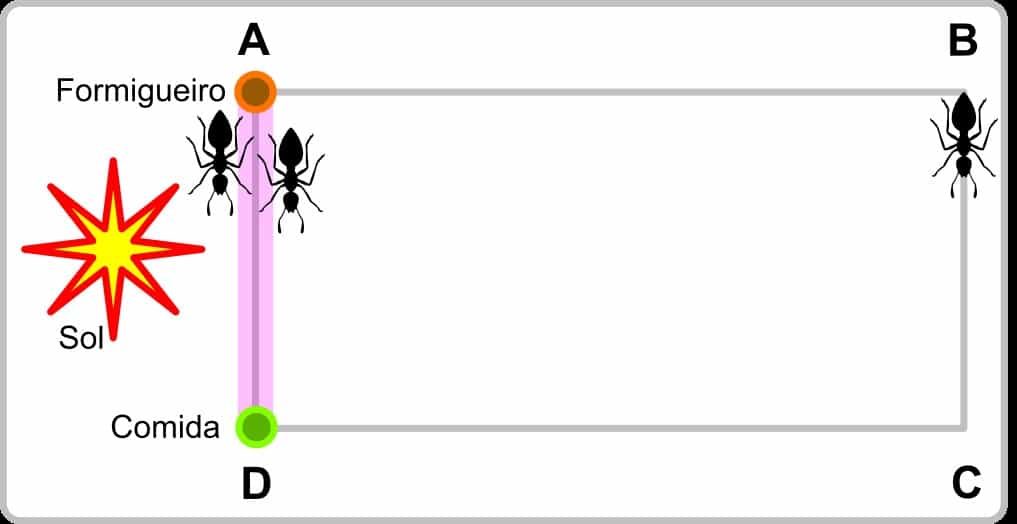
Quando chega ao formigueiro, a porção de alimento excita outras formigas que estão para sair em busca de alimentos e ao saírem, encontram o rastro de feromônio que as levam até o alimento.
Ao chegarem em D, estas formigas pegam novas porções de alimento e retornam para o formigueiro usando o rastro original como guia e o reforçam, deixando suas “pegadas” de feromônio”. Com mais formigas marcando o caminho, o odor do feromônio é reforçado, reforçando a motivação das formigas que saem do formigueiro rumo ao alimento.
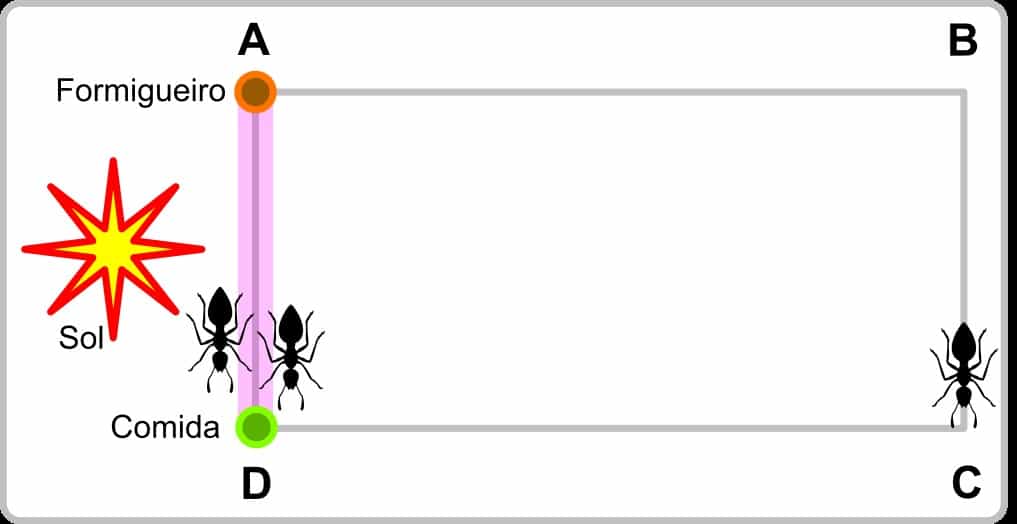
O feromônio é um elemento de comunicação e interação social entre as formigas. Quanto mais forte o cheiro do feromônio, mais formigas tendem a seguir aquele caminho. Há diferentes feromônios para diferentes tipos de interações. Há feromônios para marcar o caminho para alimento, para combate a inimigos e para a construção do formigueiro, e cada tipo diferente de formiga (operária, soldado etc.) é mais sensível de forma seletiva a um tipo de feromônio.
O feromônio afeta seletivamente o comportamento de cada formiga, mas tem duas propriedades importantes: a saturação e a volatilidade. A saturação é importante para evitar que um determinado objetivo (o alimento em D, por exemplo) crie uma atração que concentre a atenção de todas as formigas nele, tornando ineficiente a exploração deste recurso e perdendo a oportunidade de encontrar novos recursos. A volatilidade faz com que as marcas de caminho sejam apagadas ao final da exploração do objetivo (o fim do alimento em D, por exemplo), e as formigas busquem novos objetivos e recomecem esse ciclo.
Sobre a formiga que no nosso exemplo seguia o caminho A-B-C-D, se ela chegar em D antes do fim do alimento, ela se comportará como as demais, pegando um pouco de alimento e seguindo o caminho marcado de volta D-A. Se o alimento tiver acabado, ela continua sua exploração, mas nenhuma outra formiga seguirá o caminho A-B-C-D para buscar alimento por ele não foi marcado.
Se esta formiga encontrar alimento em C, ela retornará por C-B-A. A esta altura, o caminho A-D estará bastante reforçado, e a volatilidade sobre um caminho mais longo vai diminuir ainda mais a atração das formigas pelo caminho A-B-C. Ainda assim, algumas formigas seguirão o caminho. Isto cria um sistema onde todos os recursos são explorados, mas os mais próximos e fáceis de serem alcançados são explorados primeiro.
Todos sabemos que formigueiros se comportam como animais inteligentes. Boa parte desse comportamento inteligente se dá pelo sistema de feromônio das formigas, que é um algoritmo poderoso de otimização. Este algoritmo é altamente computacional e pode ser usado com eficiência em programas de computador.
A pedrinha geek da Maria moderna
Marcar o caminho com pedrinhas como Maria fazia é um comportamento ineficaz hoje em dia. Mas a Maria moderna tem algo muito melhor para a mesma função: o smartphone. A bem da verdade, os smartphones foram criados para marcarem os passos dos seus donos para que eles sejam rastreados, e para isso contam com todo tipo de sensores para isso, incluindo GPS, bússola e acelerômetros, entre outros.
Há muito dinheiro nisso. Em certo sentido, os smartphones fazem o trabalho das pedrinhas de Maria e do feromônio das formigas, mas a conectividade é quem permite que esses passos sejam seguidos em grandes centros computacionais. E é exatamente disso que precisamos.Para tal, precisaremos criar um aplicativo que leia o GPS do aparelho e use a conectividade e a capacidade de armazenamento de informações para criar um banco de dados.

Nosso aplicativo fará inicialmente algo bem simples. Durante o trajeto, a cada 500 metros o smartphone transmite a posição para um servidor central e pergunta a este servidor que outras pessoas usando o mesmo aplicativo se encontram num raio de 1 quilômetro daquela posição naquele momento. A cada nova pessoa, o smartphone envia uma mensagem com um “alô” e soma um ponto ao nome dessa pessoa em uma lista. Da mesma forma, um ponto é adicionado no smartphone da outra pessoa para o registro da primeira e retorna outra mensagem de “alô”.
Esta lista está ordenada em ordem decrescente de pontuação, de forma que no topo aparecem as pessoas que mais somaram pontos ao longo do tempo.
Digamos que num determinado dia, João instale o aplicativo no seu celular e passe a usá-lo diariamente para ir ao trabalho. No começo, ninguém aparece nas listas dele, mas ao entrar em uma grande avenida, vários usuários começam a aparecer e a pontuar. Alguns deles estão apenas de passagem, e registram poucos pontos e nunca mais serão vistos. Outros seguem por um trecho mais longo e acabam pontuando um pouco mais, e assim João vai formando sua lista, da mesma forma como ele passa a fazer parte das listas dos outros usuários.

Até então, Maria não era usuária do aplicativo e por isso não aparecia nas listas de João. Mas eis que um mês após João estar usando o aplicativo, Maria decide usá-lo também.
Maria mora próximo de João, trabalha ao lado dele, vai pelo mesmo caminho e horário. Desta forma, Maria pontua bastante no primeiro dia, deixando João bem colocado no topo da sua lista logo de cara.
Para João, entretanto, pelo uso há mais tempo, a lista dele possui outros usuários com melhor pontuação, e Maria começa lá por baixo. Com o passar dos dias, entretanto, Maria passa a somar muitos pontos a mais que os outros usuários constantes na lista de João, e o nome dela sobe gradativamente na lista ordenada, até ela figurar no topo. O nome dela emerge na lista para João.

Um fato curioso sobre o termo “emerge na lista”: a constância do percurso, do horário, e da distância entre João e Maria fazem parte de um comportamento emergente do fluxo de tráfego que eles formam. Este comportamento emergente não é exclusivo deles, mas de todos que compartilham o mesmo percurso, total ou parcialmente, no tempo e no espaço, mais especificamente, um comportamento de sincronismo.
A lista, entretanto, apresenta os dois comportamentos típicos do sistema de feromônio das formigas. Para começar, os pontos que são somados para o total da lista tem um tempo de vida, por exemplo, duas semanas. Os pontos tem dessa forma “um tempo de vida”.
Assim, um usuário que João encontrou apenas uma vez durante o mês não ficará eternamente na lista, sendo retirado após duas semanas. Este efeito é similar à volatilidade do feromônio das formigas.
Se Maria viajasse todos os dias sentada ao lado de João, haveria um número limitado de pontos que ela poderia somar na lista de João. Esta é a pontuação máxima que qualquer usuário poderia somar na lista de João em um dia. Se Maria viajasse todos os dias do lado de João, ao aplicarmos a volatilidade dos pontos (que expiram a cada 14 dias), então Maria atingiria um máximo de pontos somados que permaneceriam estáveis. Esta soma constante possui similaridade com a saturação dos feromônios das formigas.
O sistema de lista com propriedades de saturação e volatilidade dos pontos absorve uma componente ruidosa vinda do comportamento caótico do fluxo de tráfego. Maria pode ter que ir um dia no médico, e não irá pontuar nesse dia na lista de João. Isso fará com que a pontuação dela na lista de João caia um pouco durante 14 dias, mas irá se recuperar depois.
Entretanto a relação entre os dois estará bem marcada. Se Maria trocar de emprego para longe de João, entretanto, ela irá gradualmente descer na lista e estará fora dela em 14 dias.
O mecanismo da lista nos faz perceber a dinâmica do fluxo de tráfego em uma nova dimensão do tempo, muito mais lenta, e onde não percebemos suas turbulências. É como uma foto de um rio caudaloso tomada com longa exposição. A impressão é estranha, mas o comportamento médio do rio estará lá.

Quanto maior o sincronismo entre dois componentes do fluxo, mais um componente soma pontos na lista do outro, e quanto mais alta a proporção entre os pontos somados em relação aos pontos de saturação, mais um componente do fluxo estará em sincronismo com o outro. O afloramento do nome de Maria na lista de João é um comportamento emergente natural do fluxo, subproduto do sincronismo maior entre eles, observado do ponto de vista do João.
Com a volatilidade, surge uma propriedade da lista. Se Maria está sempre à mesma distância de João, os pontos que João descartar dela por terem mais de 14 dias serão compensados pelos pontos que ela somar naquele mesmo dia, e a soma dos pontos de Maria em relação a João será constante e mantendo uma proporção com a pontuação de saturação da lista de João.
O resultado é que a lista tanto de João como de Maria tendem ao longo do tempo a uma certa estabilidade, com as mesmas pessoas constando nas primeiras posições. Quanto maior a pontuação, mais fidedigno é o comportamento de um em relação ao outro e mais próximos eles estarão no fluxo de trânsito.
Podemos então deduzir uma primeira grande aplicação das listas. Se João tem um máximo de pontos que qualquer outro usuário pode fazer na sua lista, e Maria satisfaz 95% dessa pontuação, então há uma grande correlação entre o trajeto dos dois, no tempo e no espaço indicando o maior sincronismo entre eles. Isto significa que João e Maria poderiam ir juntos para o trabalho todos os dias, compartilhando o mesmo veículo. Se João der carona para Maria, isso significa economia para os dois, e um carro a menos para saturar as ruas para todos. Há grande benefício pessoal para os dois e um pequeno benefício para todos.
Dada a Teoria do Mundo Pequeno, a probabilidade não só de Joões e Marias existirem, como é bem provável que hajam mais pessoas que possam usufruir da mesma carona, gerando benefícios ainda maiores a todos.
As listas possuem outra propriedade importante na hora de definir quem é o usuário. João sempre vai pelo mesmo caminho, aproximadamente na mesma hora, assim como outros usuários. A lista dele possui poucos usuários, mas com alta pontuação para pelo menos parte do percurso feito sempre sobre as mesmas vias.
Um outro usuário que trabalhe com um veículo comercial não tem rota nem horário fixos. Embora o limite de pontos dele seja muito elevado, as listas de usuários e vias são imensas mas com pontuação muito baixa.
Esta diferença permite um cálculo de quão caótico é o comportamento de cada motorista em termos de rotas e sincronismo. Quanto menos caótico for o comportamento do motorista, mais o sistema pode se concentrar nele para orientar intervenções no fluxo de tráfego.
Participando de fluxos
Até este ponto avaliamos o sistema do ponto de vista de dois usuários bastante similares. Agora iremos avaliar esse sistema do ponto de vista de parte do fluxo.
Vamos imaginar que João e Maria atravessem do começo ao fim uma grande avenida bastante movimentada de 10 quilômetros de extensão. Esta avenida tem três faixas de rolamento e saídas e entradas a cada dois quilômetros. Nesta avenida, aparentemente, o trânsito é intenso e caótico, com gente entrando e saindo em cada ponto que a avenida permite. No meio deste caos, certamente há um fluxo de outros carros que fazem o mesmo percurso de João e Maria, mas não necessariamente no mesmo horário preciso. Uns passarão um pouco mais cedo, outros mais tarde.
Vamos criar mais dois personagens na nossa história: Pedro e Joaquim. Pedro trabalha um pouco mais distante da avenida que João, então ele tem de passar ali mais cedo se ele entrar no mesmo horário comercial que João. Ele passa tão cedo que fica fora do limite de 1 km de João. Como ele está fora do horizonte de pontuação para a lista de João, Pedro nunca consta da lista de João, mas isso não significa que ele não faça parte do mesmo fluxo.
Há ainda o Joaquim. Ele passa regularmente por esta avenida também à frente João, mas dentro do horizonte de pontuação de 1 km dele. E Pedro fica adiante de Joaquim, mas também dentro do do horizonte da lista de Joaquim. Assim, embora Pedro e João não constem das listas um do outro, ambos pertencem à lista de Joaquim. É a lista de Joaquim que liga Pedro a João dentro do mesmo fluxo.
O encadeamento de todas as listas mostra uma propriedade importante: uma parte do fluxo de tráfego pode ser interligada como uma longa corrente, onde a cadeia de elos é formada pelas listas dos vários usuários. A lista é interligada, ou melhor, encadeada. Se começarmos observando o topo da lista de Pedro, encontraremos Joaquim, e no topo da lista deste, João e Maria e assim por diante.
Esta propriedade é importante, pois começa a mostrar que parte do fluxo de tráfego é caótico apenas aparentemente, apresentando uma estrutura consistente e que pode ser mapeada através do processamento das listas individuais.
O encadeamento de usuários obtido a partir das listas revela não apenas a relação entre eles, mas uma estrutura física desta cadeia de veículos, como se ele fosse um organismo vivo, tal qual pensamos um formigueiro. Se uma pessoa ficar em um ponto fixo, verá Pedro passar, depois Joaquim, depois João e Maria, e assim por diante.
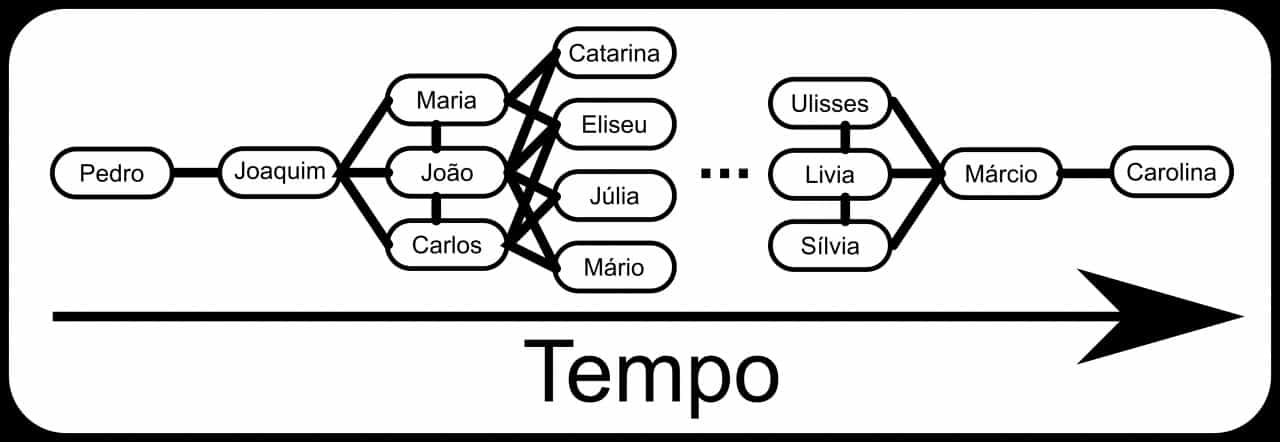
Reparem o estranho ente que estamos mapeando. Estabelecemos uma rede social, esta rede social é feita de pessoas que não se conhecem mas se relacionam todos os dias por sincronismo, e esta rede social tem uma conformação física bastante definida.
Esta cadeia de usuários tem uma propriedade muito importante. Vamos imaginar que esta cadeia fosse numerosa o suficiente para tomar toda a avenida. Pedro, Joaquim, João e Maria conforme iriam entrando à avenida iriam se integrando ao fluxo. Mas se o que define o fluxo é a constância da rota e da velocidade, mantendo sempre os mesmos carros próximos uns dos outros, dia após dia, então João e Maria estão cercados de carros que percorrerão a avenida toda juntos. Não há razão para que os carros tentem acelerar ou frear mais que os outros. Também não há razões para que os carros fiquem trocando de pista e gerando atritos internos ao fluxo.
O resultado é um fluxo granular onde todos os grãos (carros) se deslocam coesos e em perfeito sincronismo. É um fluxo consistente e com organização interna como um fluxo unificado formando um corpo como uma comprida serpente. Quando João, Maria ou qualquer membro desta cadeia entrar na avenida, irá percorrê-la do começo ao fim sem tropeços, sem retardos. Basta acompanhar o fluxo. Vamos chamar esta cadeia de “A”.
Criando soluções viárias viáveis
Vamos imaginar que a cadeia “A” circula pela avenida movimentada, em meio a um grande fluxo completamente caótico. Ela circula entre carros mais rápidos e mais lentos e que trocam de faixa aleatoriamente. O atrito no fluxo é grande entre os elementos de “A” e o resto dos veículos.
Entretanto, se colocarmos os elementos de “A” para circular agrupados, o atrito do fluxo é reduzido com benefício a todo o fluxo, mas em especial a “A”.
Este é um ponto que a velha engenharia de tráfego não contempla. Por ela tratar todos os veículos como iguais, ela não possui ferramentas para observar e lidar com esta microestrutura natural do fluxo.
Quando identificamos um subfluxo como a cadeia “A”, e o tratamos adequadamente, o resultado é uma melhoria significativa para o subfluxo e uma melhoria sensível para todo o restante do fluxo.
Mas qual a melhor forma de agrupar “A” neste caso para colhermos benefícios reais? Aqui dependeremos da conformação da avenida. Cada situação tem de ser estudada individualmente.
No nosso exemplo, a avenida tem três faixas de rolamento, numeradas de 1 a 3 da direita para a esquerda, e a cada 2 quilômetros temos uma entrada e uma saída à direita da via.
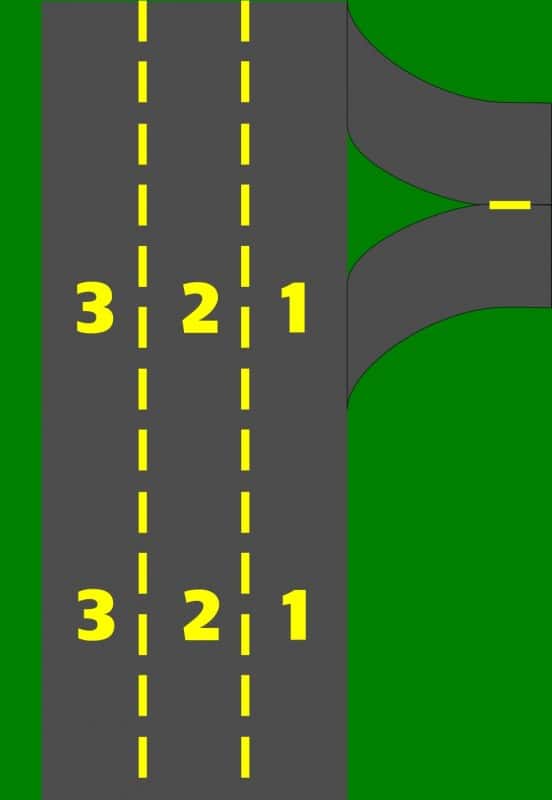
Neste tipo de avenida, quando um veículo vem pela avenida pela faixa 1 e deseja tomar a saída, ele normalmente reduz a velocidade para contornar com segurança a curva. Essa redução de velocidade impacta no fluxo que vem atrás dele, reduzindo a velocidade de boa parte da faixa 1 antes da saída.
Nas entradas, um fenômeno similar ocorre. Os carros vem da curva para a avenida em velocidade reduzida e assim entram na avenida, obrigando a quem vier pela faixa 1 em velocidade mais alta a reduzir. Isso torna a faixa 1 mais lenta.
Muitos dos carros que vêm pela faixa 1 antes da saída e desejam seguir em frente podem preferir mudar para a faixa 2. Entretanto, a tentativa de mudar da faixa 1 para 2 pode acontecer em velocidade menor que a dos carros que já estão na faixa 2, obrigando aos que estão atrás na faixa 2 a reduzirem de velocidade. Algo semelhante pode acontecer na entrada para a avenida. Assim, parte da perturbação da faixa 1 é transmitida para a faixa 2, aumentando o atrito interno ao fluxo e tornando-o mais caótico.
Em bem menor escala é a perturbação percebida na faixa 3 por causa da turbulência na faixa 1.
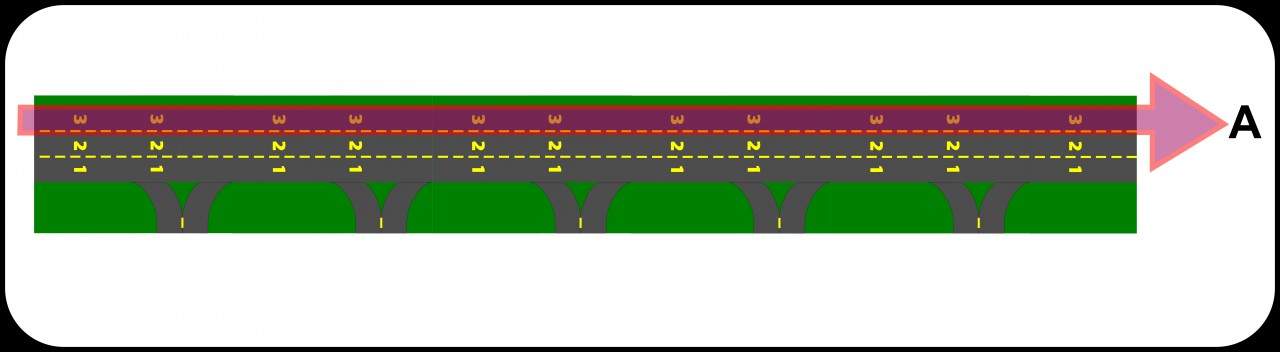
Agora vamos juntar as partes. Sabemos que o fluxo que trafega pela faixa 3 é o menos perturbado, enquanto a cadeia “A” forma um fluxo altamente consistente e colaborativo. Se agruparmos a cadeia “A” para circular pela faixa 3, não só o atrito do resto do fluxo com os elementos dela serão menores, como o atrito que “A” causa no resto do fluxo também será menor. Não somente “A”, mas todo o fluxo fluirá melhor dessa forma.
A sugestão para que o carro da cadeia “A” use a faixa 3 pode ser feita pelo próprio aplicativo. Seria uma das utilidades do aplicativo para o usuário.
Cadeias e mais cadeias
Entretanto, a estrutura do fluxo de tráfego pode ser muito mais complexo do que simplesmente definir cadeias de carros como a “A”.
Vamos imaginar que da mesma forma como definimos a cadeia “A”, exista uma cadeia “B”, que entra na avenida pela entrada do km 2 e saia no km 8. Este fluxo é coerente com a cadeia “A” do km 2 ao km 8 da avenida. Se a avenida já apresenta tráfego pesado, a entrada e a saída da cadeia “B” representa uma pequena fração de fluxo que é adicionada ou subtraída do fluxo total. Entretanto, quando “B” se junta a “A”, a parcela de tráfego altamente consistente aumenta e se torna mais significativa em relação ao fluxo total e o manejo adequado deste subfluxo maior reflete em benefícios para todo o fluxo.
Assim como as pedrinhas de Maria, cada ponto contado na lista tem um posicionamento físico que o define. A soma dos pontos por região da avenida considerando os dois fluxos mostram uma nova estrutura do fluxo total. Até o km 2 temos o fluxo “A”, quando então passamos a ter um fluxo “AB”, e que retorna ao fluxo “A” do km 8 até o fim da avenida. Temos então três cadeias bem caracterizadas ao longo da avenida.
No instante em que a cadeia “B” se soma à cadeia “A”, forma um fluxo maior com a mesma coerência interna, mas num trajeto menor da avenida. Então “B” pode ser orientada a usar a faixa 3 da avenida, diminuindo ainda mais o atrito interno e o caos do fluxo total da avenida. Dependendo do volume de tráfego de “AB”, ele pode ocupar integralmente a faixa 3, deixando as faixas 1 e 2 para o trânsito local naturalmente turbulento, e uma parcela significativa desse fluxo segue sem sofrer nem gerar interferências no fluxo total.
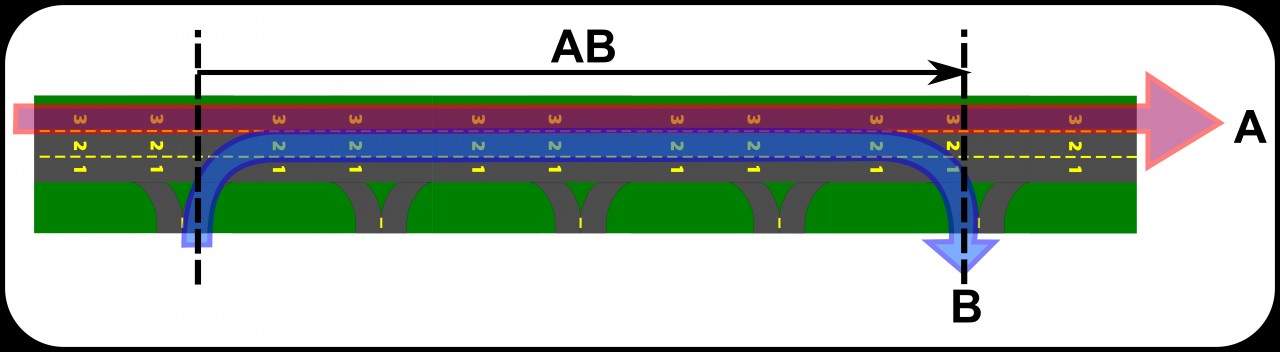
Entretanto, através do sistema de pontuação não veremos exatamente “A” e “B” porque eles verdadeiramente não existem. O que existe realmente é uma cadeia que existe no começo da avenida e segue unida até o km 2. Ali ela encontra uma segunda cadeia para formar uma cadeia maior que se sustentará até o km 8, quando então as cadeias novamente se separarão e seguirão caminhos distintos. Isso nos leva a um aperfeiçoamento das listas individuais.
O que observamos com a junção das cadeias “A” e “B” é um processo crescente de autoorganização por sincronismo dentro do fluxo de tráfego, que diminui o caos (medido na forma de entropia) do fluxo. Este fenômeno foi chamado de “estruturas dissipativas” por Ilya Prigogine, em cujo trabalho valeu-lhe o Prêmio Nobel de Química em 1977.
Entretanto, o fluxo total não é formado por apenas duas cadeias. Cada veículo segue seu próprio caminho na avenida. Quanto maior o trajeto percorrido regularmente na avenida, mais pontos este motorista acumula nas listas de outros motoristas de trajetos longos, e são aqueles com mais pontos que tornam visíveis as grandes cadeias dentro do fluxo do trânsito.
O sistema de pontuação das listas, onde os pontos possuem posição geográfica definida, permite que os grandes fluxos consistentes se destaquem pela emersão das próprias listas. Desta forma, as listas com pontos que possuam posição geográfica nos indica uma cadeia “AB” e não a soma das cadeias “A” e “B”.
Se juntarmos às informações de posicionamento geográfico dos pontos informações sobre o instante dos seus registros, podemos mapear precisamente onde e quando eles se formam, quando e onde eles se dissipam e qual a sua intensidade em relação ao fluxo total da avenida no mesmo instante.
São estes subfluxos altamente coerentes que precisamos manipular para maior eficiência do fluxo total. Lembrando que uma ineficiência local pode induzir uma maior eficiência do sistema como um todo, ou seja, podemos hora beneficiá-lo, hora atrasá-lo um pouco para uma melhoria do sistema viário como um todo.
É o mapeamento da intensidade e da localidade desses subfluxos altamente consistentes que apontam quais as melhores soluções viárias devem ser adotadas, desde ações simples como orientar que os agrupamentos andem juntos na mesma faixa de rolagem, na escolha dos tempos de semáforos ou mesmo da necessidade de grandes obras viárias.
Mesmo que os usuários com aplicativo representem uma porcentagem pequena dos veículos circulantes, já é possível ter uma boa noção dos principais fluxos coerentes de trânsito, do tamanho, do local e hora em que ocorrem. A simples amostragem já é suficiente para gerarmos resultados sensíveis na melhoria do trânsito da cidade.
A grande rede feita de redes
As cadeias do fluxo obedecem muitas das propriedades das redes de mundo pequeno, e uma das propriedades destas redes é que elas podem ser parte de redes ainda maiores.
No nosso exemplo, falamos das cadeias “A” e “B” que se juntam para formar a cadeia “AB” em um trecho da avenida. Há, entretanto, uma extrapolação possível desse modelo. Os veículos que formam estas cadeias não existem apenas dentro desta avenida. Eles vieram de algum lugar e se dirigem a algum outro lugar. É de se esperar que pela Teoria do Mundo Pequeno que a coerência que os faz pertencer à sua cadeia não se estabeleça unicamente nesta avenida, mas continue total ou parcialmente nas avenidas seguintes, até que essas cadeias se dissipem totalmente.
Assim, é de se esperar que pelo menos uma parte da cadeia “A” já esteja formada numa avenida anterior e continue estável, mesmo que parcialmente, numa avenida seguinte.
Assim, o que podemos mapear como cadeia “K” numa avenida precedente e “M” numa avenida posterior seja em parte a constituinte da cadeia “A”. Estaremos lidando com um cadeia consistente que atravessa várias avenidas antes de se dissipar, mas que se une com outras cadeias ao longo do percurso para formar subfluxos ainda mais consistentes em determinadas partes do trajeto.
É esta grande e estranha anatomia difusa do tráfego sobre a cidade, que surge do caos e revela uma estrutura interna definida, ramificada, consistente, ordenada, mutável, que se adapta às mudanças do ambiente que precisamos mapear.
Ao mapearmos todas as cadeias pelo menos das principais avenidas e como cada cadeia se relaciona com as outras cadeias das outras avenidas, passamos a ter uma melhor noção de onde a grande maioria das pessoas vem e para onde vai. Há inúmeras aplicações para estas informações, desde informações de controle viário, como sincronização de semáforos, da indicação de obras viárias, e até mesmo o estabelecimento de linhas de ônibus que atendam melhor este fluxo de pessoas.
Podemos assim criar uma grande rede onde cadeias consistentes de usuários se ligam às diferentes avenidas de toda cidade. O mapeamento destas redes nos informam de onde vem e para onde vão as grandes massas consistentes de veículos. É aqui onde nasce uma nova engenharia de tráfego.
Com o mapeamento de como os grandes fluxos de tráfego se formam e se relacionam, é possível medir e talvez até prever o impacto de uma perturbação num desses grandes fluxos.
O que acontece se criarmos um túnel que encurta uma grande volta? Vai beneficiar o trânsito local ou irá causar um gargalo em outro lugar, gerando congestionamento onde hoje isso não acontece? Qual o impacto da interdição de vias por obras do metrô e quais os melhores caminhos alternativos? Ter o mapa das principais cadeias facilita muito esse tipo de resposta.
O método parte do mapeamento do comportamento sincrônico de cada usuário e progressivamente cria uma imagem completa do comportamento dos fluxos de trânsito de toda rede viária da cidade.
Há muito mais
Há muitas questões ainda a serem feitas que precisam ser mapeadas para serem respondidas.
– Maria pode andar perto de João e ser bastante coerente com ele na ida ao trabalho. Mas e na volta? E se João vai para seu curso noturno enquanto Maria vai fazer sua aula de balé? Por esta razão podemos nos perguntar a até que ponto as cadeias dos horários de pico da manhã e da tarde são simétricos. Será que as cadeias do horário de pico da manhã são menos numerosas, mais robustas e consistentes enquanto as do pico da tarde são mais numerosas, menores e mais caóticas?
– Como a sazonalidade afeta as cadeias de tráfego? Como calor, frio, chuva, horário de verão as afeta? Que impactos podem ser observados? O que podemos fazer para antecipar e mitigar problemas? Este algoritmo aparentemente simples apenas arranhou o potencial do que pode ser explorado com um smartphone na mão de cada motorista. O que foi apresentado nesta matéria é apenas uma amostra perto do que pode ser conseguido com esta forma de pesquisa de dados.
Observação importante
Prezado leitor, pare um instante a leitura e reflita sobre o que leu até agora. Através de dados simples coletados do seu smartphone é possível estabelecer uma grande rede de relação social à qual você pertence e da qual provavelmente você não conheça ninguém com quem se relaciona quase que diariamente.
E, como me ensinou um vendedor calejado uma vez, onde as pessoas se juntam sempre tem dinheiro para quem sabe tirar proveito da situação.
Portanto, não é absurdo afirmar que as grandes empresas de tecnologia sabem mais a seu respeito do que você mesmo. Cuidado com os dados que você compartilha. Eles dizem muito mais a seu respeito do que você imagina.
Finalizando
Este é um modelo matemático pessoal, não faz parte da tradicional engenharia de tráfego, e, portanto, não pode ser encontrado nos livros sobre esse assunto. É uma técnica completamente inovadora e que merece um projeto de pesquisa e desenvolvimento.
Ele está apoiado em teorias científicas básicas com menos de 20 anos, e que vem sendo aplicadas onde as técnicas estatísticas tradicionais não dão mais conta.
Que ninguém espere que as aplicações deste modelo irá resolver completamente os problemas do tráfego, mas qualquer ganho que pudermos obter por ela sempre será uma conquista a ser comemorada.
Também o que mostrei aqui é apenas uma pequena amostra do que pode ser obtido com esta técnica de coleta de dados. Há muitos outros experimentos e certamente há muito mais a ser imaginado.
Espero que tenha rendido uma boa leitura de domingo, mostrando que de velhas historinhas infantis podem surgir soluções tecnológicas inesperadas para os problemas da modernidade.
Ah! E por que me esforcei tanto em desenvolver esse modelo? Bem, isso eu conto numa próxima oportunidade…
AAD







